목록영상처리 (8)
DevKim
 [영상처리] MATLAB 히스토그램(Histogram) : imhist, imadjust, gamma, piecewise linear
[영상처리] MATLAB 히스토그램(Histogram) : imhist, imadjust, gamma, piecewise linear
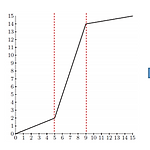
히스토그램(Histogram) - 각 밝기 값이 영상에서 존재하는 개수를 나타내는 그래프 Q) 히스토그램으로 어떤 정보를 얻을 수 있을까? 1. 화소들의 밝기 값이 낮은 영역에 많이 속하면 어두운 영상임을 알 수 있음 2. 화소들의 밝기 값이 높은 영역에 많이 속하면 밝은 영상임을 알 수 있음 3. 화소의 밝기 값이 넓은 범위에 걸쳐 분포하면 대비(contrast)가 좋은 영상(=선명함) 1. 히스토그램 구하기 imhist p=imread('pot.tif'); figure,imshow(p); figure,imhist(p),axis tight #axis tight를 사용하면 히스토그램 바가 꼭 맞게 디스플레이됨 → 밝기 값들이 넓게 분포해있지 않고 가운데에 몰려있음 → 대비가 좋지 않음 2. 히스토그램 스..
 [영상처리] MATLAB 영상처리 연산
[영상처리] MATLAB 영상처리 연산
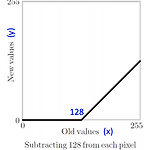
*영상처리의 연산은 화소(pixel)의 값들을 변경한다 1.변환(transform) : 전체 영상을 하나의 블록으로 생각하고 화소의 값을 변경함 2. 영역단위처리 : 이웃화소들을 참조하여 해당 화소의 값을 변경함 3. 화소 단위 처리 : 자신의 화소 값만들 사용하여 해당 화소의 값을 변경함 --> 화소 단위의 처리에서 사용되는 산술 연산에 대해 이야기해본다 * y=f(x) 이때 y는 결과 영상, x는 원본 영상 1. 덧셈(뺄셈) y=x+-C imadd,imsubtract → 밝은 쪽 정보가 손실되며, 영상이 전체적으로 밝아짐 → 어두운 쪽 정보가 손실되며, 영상이 전체적으로 어두워짐 b=imread('block.tif'); b1=imadd(b,128); #b+128 b2=imsubtract(b,128);..
 [영상처리] MATLAB 공간 해상도 & 양자화 & 디더링(Dithering)
[영상처리] MATLAB 공간 해상도 & 양자화 & 디더링(Dithering)
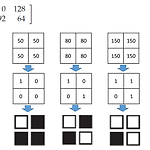
1. 공간 해상도 (spatial resolution) - 영상에 대한 화소들의 밀도 - 공간 해상도가 높을수록 더 많은 화소들이 영상의 디스플레이에 사용됨 * imresize 함수를 사용하여 공간 해상도 변경 가능 사이즈를 1/2로 줄이기위해 2*2 행렬중에 1개만 선택함 -> 그 후에 2배로 늘림 => 실제 해상도는 다르다 2. 양자화 (Quantization) : 몇 단계로 표현할거냐? - 영상의 밝기값을 표현하는 데에 사용되는 밝기값의 개수 -기본 영상은 밝기 값을 256으로 양자화한 것임 *균일 양자화 : 밝기 값의 범위를 균등하게 나누어 양자화 (1) floor(버림) 함수 사용 방법 *N개의 밝기값으로 양자화하는 경우 (2) grayslice 함수 사용 방법 2. 디더링 (Dithering)..
 [영상처리] 영상 생성 과정 : 핀홀 카메라, 칼라 영상 획득 ( CCD / CMOS /Bayer filter / Demosaicing )
[영상처리] 영상 생성 과정 : 핀홀 카메라, 칼라 영상 획득 ( CCD / CMOS /Bayer filter / Demosaicing )
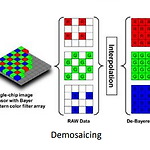
*본 포스팅은 세종대학교 '서재규' 교수님의 강의자료와 '매트랩을 이용한 디지털 영상처리의 기초' 교재를 참고하였습니다. 이번엔 영상 생성 과정에 대해 간단하게 알아보자 핀홀(pinhole) 카메라 빛이 들어오지 않는 상자와 작은 구멍으로 구성된 간단한 형태의 카메라 --> pinhole 카메라엔 trade-off가 있다 (하나가 좋아지면 하나가 나빠지는 것) 카메라에 렌즈가 필요한 이유는? 위의 그림은 작은 구멍으로 봐서 선명하지만, 빛이 적게 들어와 어두운 상을 만들고 아래의 그림은 큰 구멍으로 봐서 상은 밝지만, 구멍이 커져서 상이 여러개가 겹쳐보이게 되고, blur가 생긴다. 렌즈는 빛의 굴절을 이용하여 빛을 모아주는 역할을 하는 광학기구로, 선명하면서 밝은 상을 얻을 수 있게 도와준다. 칼라 영..
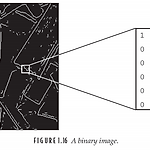 [영상처리] 디지털 영상의 타입 : binary,grayscale,true color (RGB), indexed 영상
[영상처리] 디지털 영상의 타입 : binary,grayscale,true color (RGB), indexed 영상
2진(binary) 영상 : 0과 1의 두개의 밝기값만을 갖는 영상 = 흑백 영상 그레이스케일(grayscale) 영상 : 0과 1 or 255 사이의 여러 밝기 값을 갖는 영상 천연컬러( true color) / RBG 영상 : Red & Green & Blue 의 빛의 삼원색에 대한 밝기 값을 갖는 영상 보통 256단계로 양자화가 진행이 되고, 256 = 2^8 = 8 bits 로 표현된다 --> 8 bit X 3가지 (R,G,B) =24 bits 따라서 24비트 컬러영상 = 256^3 =16,777,216 가지의 다른 컬러 값을 가질 수 있다. 인덱스( indexed ) 영상 : 저장/전송의 효율을 위해 컬러 map / 컬러 팔레트 에 대한 인덱스로 구성된 영상 --> 영상은 대부분 1600만 이상..
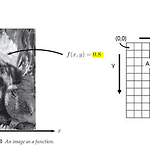 [영상처리] 영상과 디지털 영상- sampling,양자화,이웃화소
[영상처리] 영상과 디지털 영상- sampling,양자화,이웃화소
영상 = 2차원 함수 즉, f(x,y) 로 생각할 수 있다. 각 함수의 값은 주어진 점에서의 영상의 밝기를 나타냄. 즉, (x,y)는 위치이고 f(x,y)는 해당 위치의 밝기를 나타낸다. * 일반적으로 영상의 원점은 좌측상단임 영상 = 2차원 함수, 각 함수의 값들 = 그 점의 영상의 밝기 디지털 영상 : 연속적 영상에서 샘플링된 점들로 구성된 아주 큰 배열 --> 각 점들은 양자화된 특정 밝기 값을 가지고있음 이때 샘플링된 점 = 화소(pixel) = 디지털 영상을 구성하는 요소 * 샘플링 : 등간격으로 나눠서 특정한 위치에 있는 값들만 취해주는 과정 *양자화 : 밝기를 일정한 간격으로 양자화해주는 것 이웃화소(neighborhood) : 주어진 하나의 화소를 둘러싸고 있는 화소들
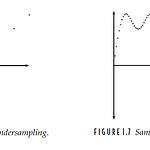 [영상처리] 영상 획득과 샘플링 Sampling
[영상처리] 영상 획득과 샘플링 Sampling
*본 포스팅은 세종대학교 '서재규' 교수님의 강의자료와 '매트랩을 이용한 디지털 영상처리의 기초' 교재를 참고하였습니다. 샘플링(Sampling)? 연속적인 함수를 디지털화하는 과정 샘플링이라는 단어만 들었을때 대충 어떤 느낌인지 감이 오지만, 더 자세하게 설명을 해보겠다. * 먼저 함수 y=sin(x)+1/3*sin(3x) 를 동일간격으로 떨어진 N개의 값으로 샘플링한다고 가정해보자. 왼쪽은 듬성듬성 샘플링, 즉 undersampling 하였고 오른쪽은 좀 더 많은 점들로 샘플링을 진행하였다. 한눈에 봐도 왼쪽의 점들로는 원래의 함수를 알아내는게 거의 불가능하다. 샘플링 이론 (Sampling theorem)? 샘플링 주파수가 적어도 해당 함수의 최대 주파수 성분의 2배 이상이 되어야만 샘플로부터 연속..

